Sizcə bir riyaziyyat sualı nə qədər çətin ola bilər ki, indiyədək öz həllini tapmasın?
Bəzən bir cümləlik görünən məsələnin onlarca səhvəlik həlli, isbatı ola bilər.
Hər biri üçün 1 milyon dollar mükafat qoyulmuş 6 ədəd isbatı tapılmayan suallar! 21 ci əsrdə hələdə belə sualların olması bir çox insana qəribə gələ bilər.
‘‘Open Problems‘‘ deyilən bu sualları hətda başa düşmək üçün belə riyaziyyatla bağlı bir çox məlumat sahibi olmalısız.Belə suallardan ən məşhurları Alman riyaziyyatçısı David Hilbertin 1900-cü ildə yayımladığı 23 sualı və Clay Mathematics Institute’nin Millennium Prize Problems 7 mükafatlı sualıdır.
Hər biri üçün 1 milyon dollar mükafat qoyulan suallardan 6sı hələdə öz həllini gözləyir.
Bu suallardan yalnız biri Poincare hipotenizi 2002-ci ildə rus riyaziyyatçısı Qriqori Perelman tərəfindən həll olunduqdan 4 il sonra 2006-cı ildə qəbul olunmuşdur, ancaq Grigori 1 milyon dollar və riyaziyyat sahəsinin nobeli sayılan Fields mükafatından imtina etmişdir.

Poincare hipotenizi: Qapalı iki ölçülü səthlər üzərində hər bir çevrə bir nöqtəyə büzüşə bilirsə bu səth kürədir. Poincare hipotenizi həmin vəziyyətin üç ölçülü səthdə də eyni olduğunu iddia edir.
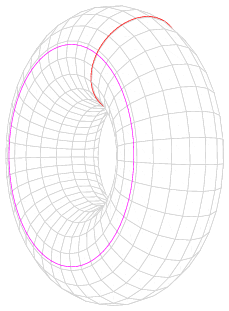
Grigori cavab olaraq bu şəkili çəkmişdir: rəngli çevrələrin heç biri səthdən ayrılmadan bir nöqtəyə büzüşməz.
Open Problems’ dən olan suallaradan biridə: tək sayda mükəmməl ədədlər varmı?
Mükəmməl ədəd özü xaric bütün müsbət bölənlərinin cəminə bərabər ədəddir.Başqa cür desək mükəmməl ədəd bütün müsbət bölənlərinin cəminin yarısına bərabərdir.
Məsələn 6 mükəmməl ədəddir 1+2+3=6. Bunun üçün Evklidin 2p−1(2p−1) düsturundan istifadə etmək olar (burada p sadə ədəddir).
p = 2: 21(22−1) = 6
p = 3: 22(23−1) = 28
p = 5: 24(25−1) = 496
p = 7: 26(27−1) = 8128
Bu zaman cüt mükəmməl ədədlər alınır. Sual olunur: tək sayda mükəmməl ədəd varmı? Bir çoxları az sayda və ya heç olmadığını düşünürlər.
Bu tipli suallardan biridə əkiz ədədlərlə bağlıdır. Fərqləri 2 ə bərabər olan iki sadə ədədə əkiz ədədlər deyilir (n və n+2). Məsələn 3 və 5, 5 və 7, 11 və 13.
Buradakı problem isə sonsuz ədədlər içərisində əkiz ədələrin omasının hələdə isbat olunmamasıdır.
Zaman-zaman bir çox insanlar məşhur olmaq üçün həllini tapdıqlarını iddia edərək müxtəlif televiziya verlişlərinə qonaq olurlar.
Bu tipli suallar elimin bir çox sahəsində mövcuddur.










